The mathematics navigation system is primarily a guideline for elementary schools to develop and achieve the milestones of arithmetical core contents. This includes a secured knowledge of numbers as well as the ability to flexibly use the four basic arithmetic fundamentals. The navigation system defines minimum standards for these five domains and therefore determines what a student needs to accomplish at the end of fourth grade in order to proceed successfully at secondary school. A minimum standard consists of several so-called basic competences. They are meant to be acquired systematically in a successive order. In the present concept the term is two-folded: On the one hand, it means to gain a fundamental understanding of numbers and arithmetical operations as well as an insight into arithmetical coherences. On the other hand, it implies to be confident when calculating with the four basic operations. Thus, for being successful in mathematics it is not only sufficient to have a secured knowledge about arithmetical concepts but it also requires an automatization in producing individual facts. After acquiring a basic notion of arithmetical coherences, certain facts (e.g.: the multiplication table) need to be secured in the long-term memory as well, so that they can be recalled without much effort (of time, imagination, concentration and thinking). The purpose of the navigation system is to find a balance between imagination and automatization. Before a minimum standard is fully achieved all the basic competences need to be applied to arithmetical problems (also taken from everyday life) in order to prove whether the newly gained knowledge and skills are helpful or not.

The mathematics navigation system, however, is more than just a framework to support further development. In order to be genuinely valuable to math teachers, several materials have been published:

1. The navigation system MathNav: It provides a supporting framework which lists necessary basic competences that should be gained during math lessons at elementary school in a hierarchic order and thus determines successive learning steps.
2. The manual: It provides explanations about every basic competence. It explains the purpose and relevance of each one, how to assess whether or not it is already managed and how to support a student if he or she cannot master certain skills yet.
3. Diagnostic sheets: They facilitate the diagnostic procedure as they help to assess most of the basic competences. In other cases, a teacher has to be present to test certain competences, for instance when focusing on automatization processes or working with quantities. Nonetheless, assisting materials are available for every examining situation so that there is no need for any further preparation time in order to identify the students’ states of knowledge.
4. Templates: Helpful copies for teaching and learning arithmetical concepts are provided and therefore always at hand when needed in the classroom. The manual explains which template has to be used for the currently examined basic competence.

Please note: The development of the mathematics navigation system is currently in progress and therefore hasn’t been published yet. At present it can only be used project internally.

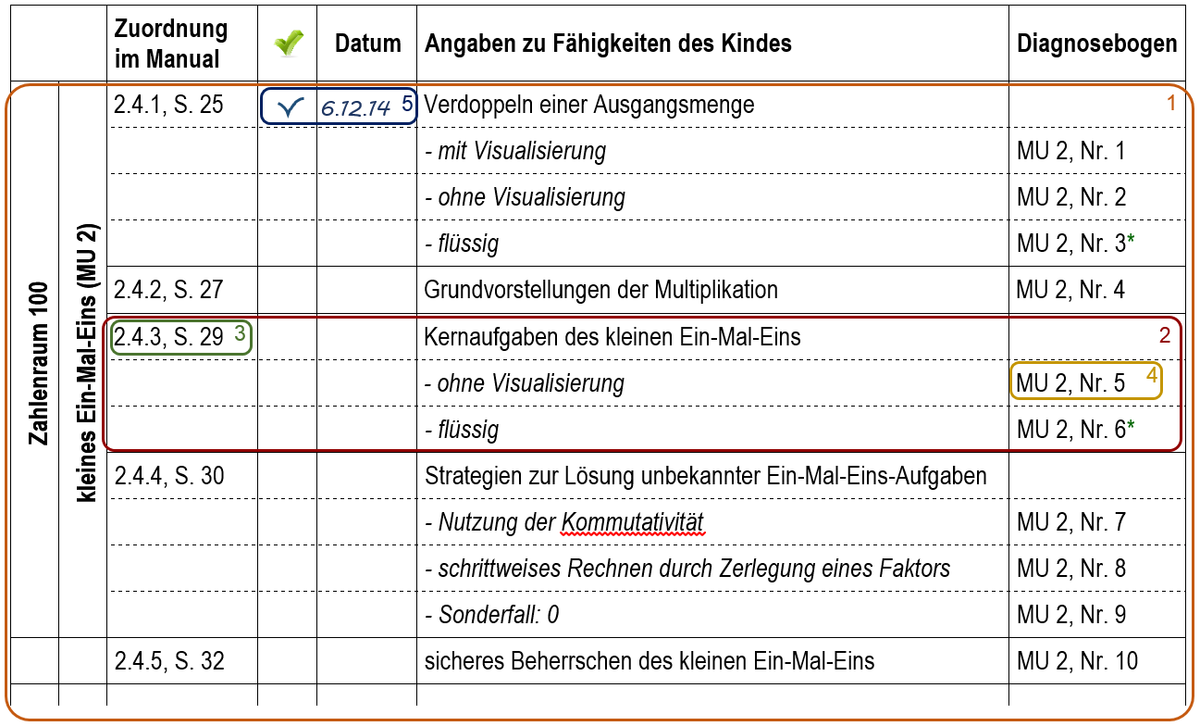
1. The orange-coloured frame shows an extract of basic competences to be achieved in grade 2. The MathNav is organised according to the order in which the different ranges of numbers are taught in each grade. In this way students will gain the appropriate competences until the end of the school year (minimum standard): In grade 1 this includes competences that are assigned to the numbers until ten first and then to the numbers until 20. In grade 2 they are extended to the numbers until 100, in grade 3 to numbers until 1000 and in grade 4 competences are determined for the range of numbers within the millions. For each range of numbers the students acquire the appropriate basic competences first and afterwards they learn the basic calculating operations.
2. The red frame shows a chosen basic competence. In order to assess whether a child has already adopted it or not, the teacher can check if it genuinely understands the particular arithmetical concept with the help of a visual aid. Afterwards, the teacher examines if the student is also able to solve the problem without a visual aid. There are multiple basic competences that should not only to be understood but that also have to be mastered by heart. As a last step, the teacher assesses how fluently the students apply the newly gained skills.
3. In the green frame basic competences are connected with the MathNav manual. This assures a quick access to all the necessary explanations for teachers.
4. In the yellow frame single aspects of a basic competence are assigned to diagnostic sheets. Sheets that have an asterisk (*) attached to it are only to be practiced on in the presence of a teacher. The manual prescribes on what the teacher should focus his or her observation during the test. There are no diagnostic sheets for individual exercises. The manual provides information about the further procedure so that the teacher can assess the availability of a basic competence.
5. The blue frame shows how the availability of a basic competence has to be entered into the system. The last check mark on the list indicates the current state of knowledge. Entering each date when the student has actually learned helps to reconstruct and visualize the learning process.

It is inevitably necessary to operate with the navigation system in a well-organized and structured way. As shown above, the teacher works straight-away through the list of basic competences and can therefore identify the present state of knowledge. Any further learning objectives will emerge automatically. By and large, the navigation system serves as an overview that shows what the students have already learned and what they still have to learn until the end of the school year. For examining the current state of knowledge at the beginning of a school year the teacher always has to start again at the top of the list, even for older students in third or fourth grade. By doing this, it becomes easier to detect learning deficits and when the child is not able to follow the lessons any more. Therefore, the navigation system has the remarkable advantage to find any ‘leaks in the basement’ so that the possible reason can be found why a student shows certain learning difficulties. As matter of fact, teachers will surely examine that especially older students did not gain any secured basic competences for the range of numbers until 20. Even though they were taught in the first grade, the necessary automatization for further calculating may not be available. Accordingly, it doesn’t come as a surprise that those children often still calculate by counting.